Analysis of Absorbance (Abs)
¡Los gráficos interactivos pueden tardar en cargar!
Key Findings and Interpretation
The regression model for absorbance (Abs) is statistically significant (P-Value = 0.000) and provides a good fit for the data, explaining 73.94% of the variability (R-sq). The analysis indicates that the formulation components have a considerable impact on the material's absorbance properties.
The most influential factor by a significant margin is Spiruline, which has a very strong positive effect. The interaction between Spiruline*Calcium (P=0.000) is also highly significant, indicating that the effect of spiruline is modulated by the calcium concentration. NPs show a strong negative linear effect. Other significant terms include the two-way interactions of Water*Spiruline (P=0.027), suggesting a synergistic effect between these two components. Encouragingly, the model shows no significant Lack-of-Fit (P=0.504), which validates that the chosen model structure is appropriate for the data. The predictive power is reasonable, with an R-sq(pred) of 61.31%.
Regression Equation
The relationship between the components and the absorbance response is described by the following equation, where the process variable Calcium is coded (-1 for 1%, +1 for 5%):
Model Goodness-of-Fit
The statistical model provides a good fit to the experimental data. The key metrics from the "Model Summary" table are:
- R-sq = 73.94%: The model explains approximately 74% of the variation in the absorbance data, indicating a strong relationship.
- R-sq(adj) = 67.86%: The adjusted R-squared is reasonably high, suggesting the model is not overfitted with unnecessary terms.
- R-sq(pred) = 61.31%: The predicted R-squared indicates a good capability for predicting new observations.
- S = 0.160046: The standard error of the regression is at an acceptable level.
The overall regression model is highly significant (P-Value = 0.000), and importantly, the lack-of-fit test is not significant (P=0.504), which increases confidence in the model's adequacy.
Model Summary: Stepwise Selection
The following table shows the stepwise selection process for the final model. The last row, highlighted, represents the chosen model with the best combination of explanatory and predictive power.
| Step | S | R-sq (%) | R-sq(adj) (%) | R-sq(pred) (%) |
|---|---|---|---|---|
| 1 | 0.215432 | 46.48 | 41.76 | 31.66 |
| 2 | 0.189003 | 60.02 | 55.17 | 47.05 |
| 3 | 0.171596 | 68.04 | 63.05 | 55.95 |
| 4 | 0.165881 | 71.07 | 65.47 | 58.92 |
| 5 | 0.160046 | 73.94 | 67.86 | 61.31 |
Model Diagnostic Plots
To ensure the validity of the statistical model, a series of diagnostic plots were generated. These plots help confirm that the assumptions of the regression analysis are met. Below is a guide to interpreting each plot:
- Normal Probability Plot: This plot checks if the residuals are normally distributed. The goal is to see our experimental points fall closely to the theoretical straight line. Significant deviations may indicate that the assumption of normality is not met.
- Residuals vs Fits: This plot is used to detect non-constant variance, missing terms, or outliers. The points should be randomly scattered around the horizontal line at zero. Any clear pattern would suggest a problem with the model.
- Histogram of Residuals: This provides another visual check for the normality of residuals. The distribution should be roughly symmetric and bell-shaped, centered around zero.
- Residuals vs Order: This plot helps to verify that the residuals are independent of one another. The data points should show no discernible trend or pattern. Any systematic pattern could suggest that the order of the experiments influenced the results.
Pareto Chart of Effects
The Pareto chart visually ranks the importance of each factor and interaction on the absorbance response. The red line indicates the threshold for statistical significance (α=0.05). Effects that cross this line are considered the most influential drivers of the process.
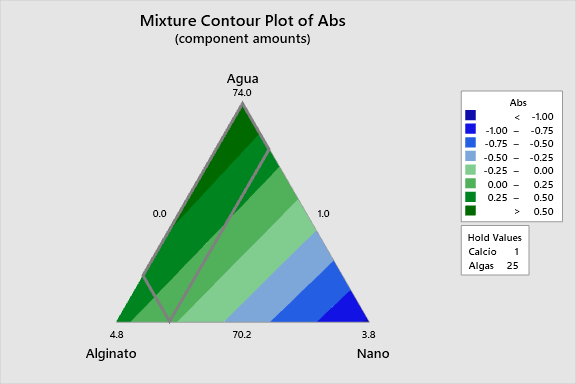
2D Contour Plots
The following interactive 2D contour plots show how pairs of variables influence absorbance while holding the other factors at constant levels. These maps are essential for identifying optimal regions in the formulation space.
3D Surface Plots
These interactive 3D plots provide an intuitive view of the response surface. Each colored surface represents the predicted absorbance response based on the model for a specific combination of held factors.
Overlaid on the surfaces are the data points from the actual experiments. The solid dots (●) represent the actual, measured absorbance values, while the crosses (+) show the values predicted by the model for those same experimental conditions. The vertical distance between a dot and its corresponding cross represents the residual error for that point. A good model will have these points lying close to the surface, indicating small errors.